



- Risset, J. C., & Mathews, M. V. Analysis of musical instrument tones. Physics Today, 1969, 22 n° 2, p23-30;
- Risset, J. C. An introductory catalog of computer-synthesized sounds. Bell Laboratories, Murray Hill, New Jersey, 1969 (réédité avec exemples sonores sur CD in The historical CD of digital sound synthesis, Mainz, Germany: Wergo, 1995);
- Pierce, John. Le son musical : musique, acoustique et informatique. Paris : Bibliothèque Pour la science : Belin, 1984.
- Mathews, Max ; Pierce, John (dir). Current Directions in Computer Music Research. Cambridge, Massachussets : MIT Press, 1989.
- Gather (John-Phillipp), The Amsterdam Catalogue of Csound Computer Instruments, éd. J.P. Gather, Université de Buffalo, 1995.
- Sousa Dias, A. D., Deux contributions à la pédagogie de la musique électroacoustique et de l'informatique musicale. Actes des Journées d'informatique Musicale, Lyon, JIM07, Lyon, Grame, 2007.
Ce catalogue, effectué dans un but pédagogique à la demande de Max Mathews en 1969, est un outil unique, très diversifié, détaillant l'utilisation de MusicV pour la production de sons de synthèse. De nombreuses techniques de synthèse originales y sont présentées ainsi que des modèles de production de divers sons instrumentaux. Ce catalogue est suffisamment documenté pour permettre la reconstitution des algorithmes et produire les mêmes sons soit en utilisant le même programme, soit dans d'autres environnements.
1. Flûte (#100)
L'exemple de la flûte indique comment le contrôle des modulations périodiques et aléatoires de l'amplitude d'un oscillateur permet d'introduire un phrasé dans une suite de notes. CSOUND
Sousa Dias, A. D. (2007), Deux contributions à la pédagogie de la musique électroacoustique et de l'informatique musicale. Actes des Journées d'informatique Musicale, Lyon, JIM07, Lyon, Grame, 2007.
2. Clarinette (#150)
Avec l'exemple de la clarinette, Jean-Claude Risset montre que la synthèse par distorsion non linéaire du signal est une technique qui permet d'exercer un contrôle global sur la richesse spectrale du son.
3. Trompette (#200 #201 #210 #250)
L'exemple de la trompette, réalisé par synthèse additive, a ouvert la voie aux techniques de synthèse par règles.
Cet exemple a démontré que l'identité d'un timbre dépend beaucoup plus des relations qui lient les différents paramètres de la synthèse entre eux, que des valeurs fixes de ces mêmes paramètres.
Les travaux de Jean-Claude Risset ont mis en évidence des caractéristiques importantes du son de la trompette :
4. Sons inharmoniques et bruités (#400 #410 #411 #420 #430 #440 #490)
Dans son catalogue, Jean-Claude Risset a également exploré le domaine des sons inharmoniques et bruités à travers la synthèse de nombreux sons de cloches et de percussions. Il décrit comment utiliser des bandes de bruit blanc ajoutées à des oscillateurs ou comment produire des spectres inharmoniques à partir d'un oscillateur périodique de fréquence infra-sonique.
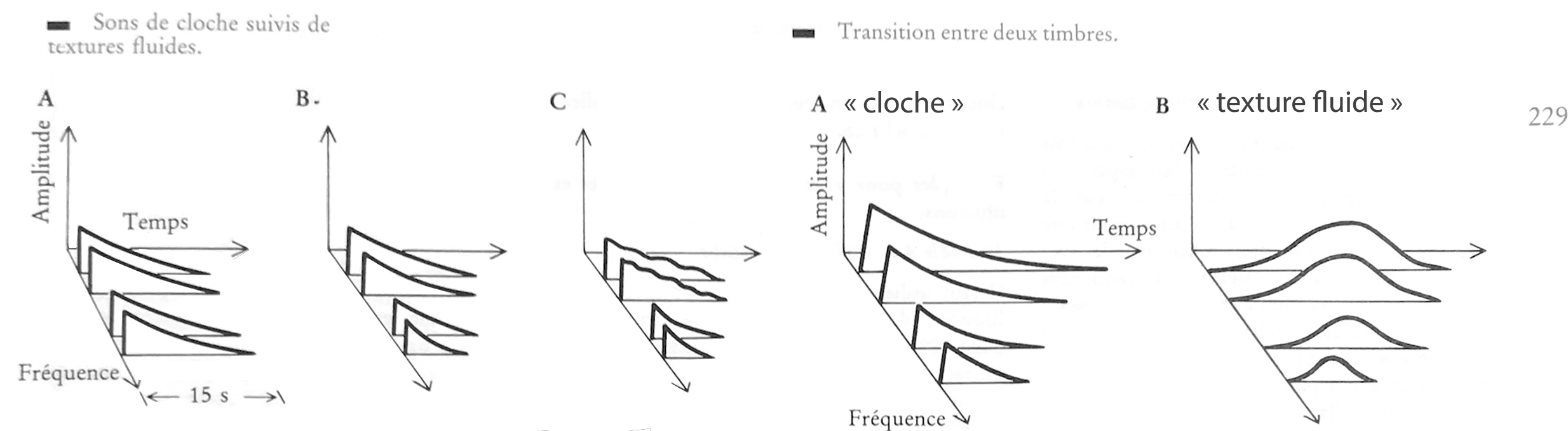
Le Son Musical, John Pierce, Coll. Pour la Science, 1983.
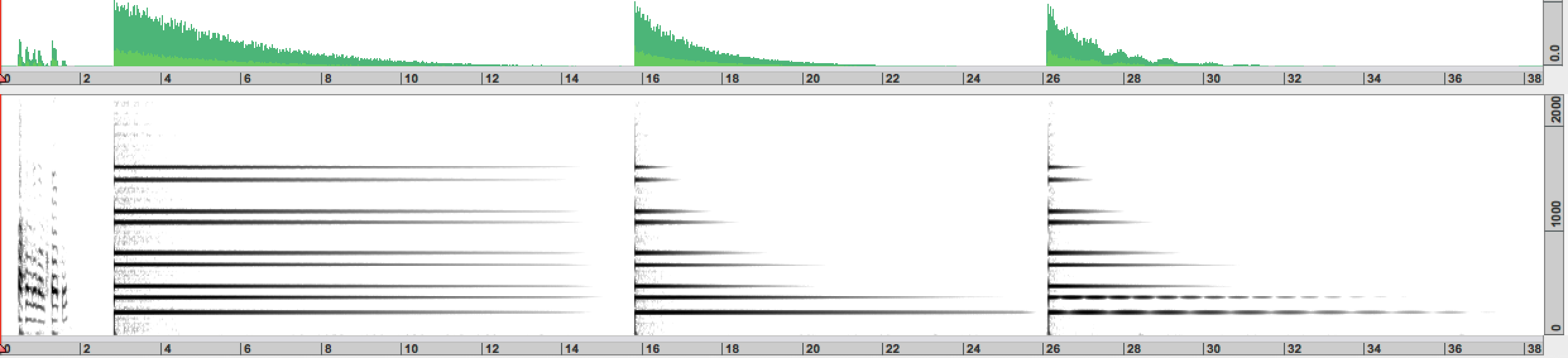
#430 : Trois approximations successives d'un son de cloche. 26 s. MP3 WAVE FAUST CSOUND
Sons produits par synthèse additive aux Bell Laboratories dans les années 60.
Sons de synthèse imitant des cloches et leur transformation en textures fluides. 24 s. MP3 WAVE FAUST CSOUND
"On entend d'abord des sons composés comme des accords et évoquant des cloches.
Puis ces objets sonores distincts se dissolvent en textures fluides, tout en conservant la même harmonie sous-jacente.
La synthèse rend facile cette transformation intime, qui préserve l'harmonie en modifiant l'allure."
COMMENT-----------------JCR430---------------- ;
COMMENT:BELL EXPERIMENTS;
COMMENT: ON TAPE M1485 FILE 4;GEN 0 5 3;
COMMENT: 5 KC SAMPLING RATE; SIA 0 4 5000;
INS 0 1;OSC P5 P7 B3 F2 P30;OSC B3 P6 B3 F1 P29;
OUT B3 B1;END;
COMMENT: TO SET GENERAL CONVT;
SV2 0 10 2 6 -7;
COMMENT: SYNCHRONOUS DECAY;
NOT 1 1 20 250 224.5 20;NOT 1 1 20 400 368.5 20;
NOT 1 1 20 400 476 20;NOT 1 1 20 250 684 20;
NOT 1 1 20 220 800 20;NOT 1 1 20 200 1096 20;
NOT 1 1 20 200 1200 20;NOT 1 120 150 1504 20;
NOT 1 1 20 200 1628 20;SEC 21;
COMMENT: NON SYNCHRONOUS DECAY;
NOT 1 1 20 250 224 20;NOT 1 1 12 400 368.5 12;
NOT 1 1 6.5 400 476 6.5;NOT 1 1 7 250 680 7;
NOT 1 1 5 220 800 5;NOT 1 1 4 200 1096 4;
NOT 1 1 3 200 1200 3;NOT 1 1 20 15015042 ;
NOT 1 1 1.5 200 1628 1.5;
SEC 21;
COMMENT: NON SYNCHRONOUS DECAY AND TWO SPLIT
PARTIALS;
NOT 1 1 20 1500 224 20;NOT 1 1 18 1000 225 18 ;
NOT 1 1 13 1500 368 13;NOT 1 1 11 2700 369.7 11;
NOT 1 1 6.5 4000 476 6.5;NOT 1 1 7 250 680 7;
NOT 1 1 5 2200 800 5;NOT 1 1 4 200 1096 4;
NOT 1 1 3 200 1200 3;NOT 1 1 2 150 1504 2;
NOT 1 1 1.5 200 1628 1.5;
TER 22;
5. Harmonies-timbres (#500 #501 #550)
Le catalogue se termine par des exemples dans lesquels l'harmonie créée par un accord se prolonge en timbre. Ceci est obtenu en faisant évoluer les notes d'un accord vers les partiels d'un spectre.
#550 : un même motif traité comme mélodie, comme harmonie et comme timbre. 10 s. MP3 WAVE FAUST CSOUND
"Le coup de gong qui fait écho à l'arpège puis à l'accord crescendo-decrescendo n'est pas analysable auditivement, mais on reconnaît qu'il prolonge l'harmonie qui précède. J'ai repris cette idée au début de ma pièce Mutations de 1969" (CD INA-C1003).

6. Sons paradoxaux (#513 #514)
Des sons abstraits sont également présentés dans le catalogue. Grâce à la synthèse de ses sons paradoxaux, Jean-Claude Risset a mis en évidence l'opposition entre hauteur spectrale et hauteur tonale. Il a reproduit les illusions de Shepard, en version continue, avec des sons qui semblent monter vers les aigus indéfiniment mais qui, en fait, restent toujours dans le même registre, et il a synthétisé des séquences qui montent la gamme pour arriver à un point bien plus grave que le point de départ. Il a également réalisé des sons qui paraissent descendre d'un demi-ton lorsque leurs fréquences sont doublées. D'une façon similaire, il a réussi à produire des rythmes qui paraissent ralentir lorsque l'on double leur vitesse.